Типовые задачи

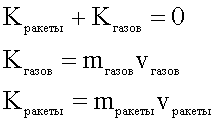
Какую скорость приобретает ракета массой 600 г, если продукты горения массой 15 г вылетают из нее скоростью 800 м/с?

Краткая теория:

Реактивное движение основано на законе сохранения импульса. Саму ракету можно рассматривать как тело, разделившееся на две части, одна из которых отброшена назад (силой пороховых газов, пружиной, сжатым воздухом), а другая устремилась вперед.

Формулы для решения:

Для изначально покоившейся ракеты в проекциях на направление ее движения можно записать:

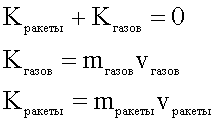
Учитывая в формулах знаки проекций скоростей ракеты и газов - они разнонаправлены, получим:

Алгоритм решения типовой задачи:

1. Кратко записываем условие задачи.
2. Изображаем условие графически в системе отсчета, где ось совпадает с направлением движения тела, а отсчет времени начинается в момент старта ракеты.
3. Записываем закон сохранения импульса для движения ракеты.
4. Решаем уравнения в общем виде.
5. Подставляем величины в общее решение, вычисляем.
6. Записываем ответ.

Возможные особенности задач:

Примеры решения:

Задача 1.

Какую скорость приобретает ракета массой 600 г, если продукты горения массой 15 г вылетают из нее скоростью 800 м/с?

1. Кратко записываем условие задачи.

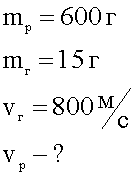
2. Изображаем условие графически в системе отсчета, где ось совпадает с направлением движения тела, а отсчет времени начинается в момент старта ракеты.

3. Записываем закон сохранения импульса для движения ракеты.

4. Решаем уравнения в общем виде.

5. Подставляем величины в общее решение, вычисляем. Перед подстановкой переводим все величины в систему СИ.

6. Ответ: скорость ракеты 200 м/с.