1. Какой формулой будет выражаться закон гармонического колебания для математического маятника, если амплитуда равна 40 см, а частота колебаний 0,5 Гц.
2. Какой формулой будет выражаться закон гармонического колебания для пружинного маятника, если амплитуда равна 10 см, а частота колебаний 2 Гц.
3. Уравнение гармонического колебания имеет вид
![]() .
.
Найти координаты тела через 0,5 сек, через 1 сек, через 2 сек после начала движения.
Гармонические колебания - это такие периодические движения, при которых координата колеблющейся точки зависит от времени по закону:
![]()
При описании движения с помощью функции "cos" надо помнить, что в нулю времени соответствует амплитудное значение координаты. Это естественно: отвели маятник в сторону, отпустили его, этот момент считаем началом движения. Начало координат при этом удобно и естественно располагается в точке равновесия маятника.
Характеристики колебательного движения:

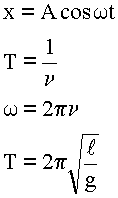
1. Кратко записываем условие, изображаем его графически. На рисунке показываем силы, действующие на колеблющееся тело и направление его движения.
2. Записываем основные формулы для колебательного движения, в которые входит искомая величина. Определяем, какие величины надо найти из других механических соотношений.
3. Решаем полученные уравнения в общем виде.
4. Подставляем данные, вычисляем. Перед подстановкой переводим все данные в единую систему.
5. Записываем ответ.
Какой формулой будет выражаться закон гармонического колебания для математического маятника, если амплитуда равна 40 см, а частота колебаний 0,5 Гц.
Решение.
1. Кратко записываем условие, изображаем его графически. На рисунке показываем силы, действующие на колеблющееся тело и направление его движения.
|
|
|
2. Записываем основные формулы для колебательного движения, в которые входит искомая величина. Определяем, какие величины надо найти из других механических соотношений.
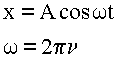
Никаких других величин искать не надо.
3. Решаем полученные уравнения в общем виде.
![]()
4. Подставляем данные, вычисляем. Перед подстановкой переводим все данные в единую систему.
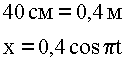
5. Ответ: ![]()
Какой формулой будет выражаться закон гармонического колебания для пружинного маятника, если амплитуда равна 10 см, а частота колебаний 2 Гц.
Решение.
1. Кратко записываем условие, изображаем его графически. На рисунке показываем силы, действующие на колеблющееся тело и направление его движения.
|
|
|
2. Записываем основные формулы для колебательного движения, в которые входит искомая величина. Определяем, какие величины надо найти из других механических соотношений.
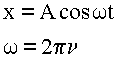
Никаких других величин искать не надо.
3. Решаем полученные уравнения в общем виде.
![]()
4. Подставляем данные, вычисляем. Перед подстановкой переводим все данные в единую систему.
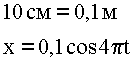
5. Ответ: ![]()
Уравнение гармонического колебания имеет вид
![]() .
.
Найти координаты тела через 0,5 сек, через 1 сек, через 2 сек после начала движения.
Решение.
1. Кратко записываем условие, изображаем его графически. На рисунке показываем силы, действующие на колеблющееся тело и направление его движения.
|
|
|
2. Записываем основные формулы для колебательного движения, в которые входит искомая величина. Определяем, какие величины надо найти из других механических соотношений.
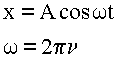
3. Решаем полученные уравнения в общем виде.
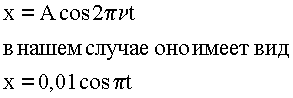
Это самое настоящее уравнение движения, по которому мы находим координаты тела в любой момент времени.
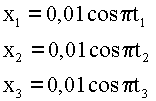
4. Подставляем данные, вычисляем. Перед подстановкой переводим все данные в единую систему.
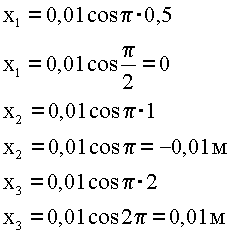
5. Ответ: Через 0,5 секунды после начала движения маятник пройдет положение равновесия, через 1 секунду – достигнет крайней амплитудной точки, через 2 секунды – вернется в начальную амплитудную точку движения.