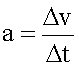
где дельта-v - изменение скорости, произошедшее за время дельта-t.
1. Ускорение автомобиля равно 3 м/с2. Как правильно по-русски прочитать эту величину и что она означает?
2. Ускорение автомобиля равно -3 м/с2. Что это означает?
3. На скоростных испытаниях автомобиль набрал с места скорость 100 км/час за 7 секунд? С каким ускорением двигался автомобиль на этом участке?
4. Пассажирский поезд, шедший на перегоне со скоростью 60 км/час затормозил перед мостом до скорости 20 км/час за 3 минуты? Каково было ускорение поезда на участке торможения?
Равнопеременное движение - это движение, при котором скорость точки (тела) за любые равные промежутки времени изменяется на одну и ту же величину. Если это движение происходит по прямой, то это прямолинейное равнопеременное движение.
Изменение скорости в единицу времени называется ускорением. Обычно оно обозначается латинской буквой "a".
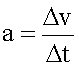
где дельта-v - изменение скорости,
произошедшее за время дельта-t.
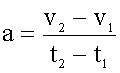
Ускорение "a" - величина векторная. При прямолинейном движении ее направление зависит от знака изменения скорости дельта-v. Принято считать, что направление координатной оси для ускорения "a" совпадает с направлением координатной оси для скорости. В этом случае, при разгоне ускорение положительно, при торможении - отрицательно.
При решении задач всегда рассматриваются не сами вектора ускорения, скорости и перемещения, а их проекции на координатные оси.
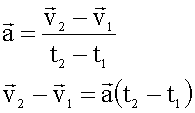
Если начальная скорость в
начальный момент времени равна нулю, то есть, ![]() ,
,
то ![]()
Пройденный путь (с учетом его направления), а при прямолинейном движении - перемещение:
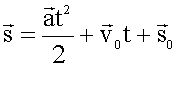
Если начало отсчета времени
и начало пути совпадают, то 
Если начальная скорость равна
нулю, то 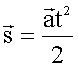
Все эти формулы справедливы в проекциях на любые координатные оси и при решении задач используются именно уравнения в проекциях:
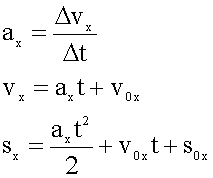
1. Кратко записать условие задачи.
2. Изобразить графически движение, указав пройденный путь и обозначив стрелками скорость, ускорение, направление движения.
3. Ввести систему отсчета, введя начало отсчета времени и выбрав оси координат для движения, скорости и ускорения. Лучше выбрать их совпадающими по направлению и направить вдоль направления движения, а отсчет времени начать в момент нахождения точки в нуле координат.
4. Записать уравнения движения на основе формул из числа вышеуказанных. Уравнения движения - это зависимость пути от времени и зависимость скорости от времени. Записать эти уравнения в проекциях.
5. Решить уравнения в общем виде.
6. Подставить величины в общее решение, вычислить.
7. Записать ответ.
В некоторых задачах часть членов уравнения движения обращается в ноль, если они равны нулю в момент начала отсчета времени.
Во многих задачах условия даны в разных системах единиц. Например, часто скорость дается в км/час, а время - в секундах. В таких задачах надо обязательно привести единицы к единой системе. Не важно, к какой, важно, чтобы к единой.
Примеры решения:
Ускорение автомобиля равно 3 м/с2. Как правильно по-русски прочитать эту величину и что она означает?
Решение.
По определению ускорение - это прирост скорости за единицу времени. Единица времени в данном случае - секунда, то есть измеряется прирост за секунду. Скорость измерена в метрах в секунду. Получается, что правильно читается так: "Три метра в секунду за секунду".
Ускорение автомобиля равно -3 м/с2. Что это означает?
Решение.
Ускорение отрицательно. В общем случае положительное направление координатной оси ускорения совпадает с направлением скорости. Тогда знак минус означает, что скорость уменьшается на три метра в секунду за каждую секунду движения.
На скоростных испытаниях автомобиль набрал с места скорость 100 км/час за 7 секунд. С каким ускорением двигался автомобиль на этом участке?
Решение.
Решаем по алгоритму.
1. Кратко записываем условие задачи.

2. Изображаем графически движение, указав пройденный путь и обозначив стрелками скорость, ускорение, направление движения.
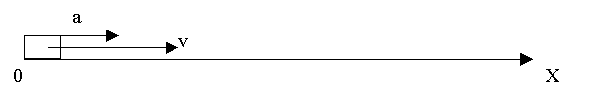
3. Вводим систему отсчета.
Ввели ее в предыдущем пункте, выбрав на рисунке ось и ноль.
4. Записываем уравнения движения на основе формул из числа вышеуказанных. В данном случае у нас одно уравнение: зависимость скорости от времени.
![]()
5. Решаем уравнение в общем
виде: 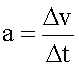
6. Подставляем заданные величины в общее решение, вычисляем. Перед подстановкой переводим скорость, заданную в км в час, в скорость, измеренную в метрах в секунду, так как время у нас задано в секундах.
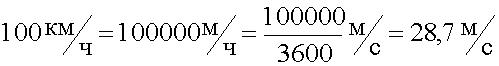
3600 - это количество секунд в одном часе.
Подставляем: 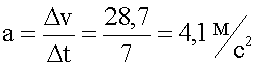
7. Записываем ответ.
Ответ: ускорение автомобиля во время разгона было 4,1 м/с.
Пассажирский поезд, шедший на перегоне со скоростью 60 км/час затормозил перед мостом до скорости 20 км/час за 3 минуты? Каково было ускорение поезда на участке торможения? Какова длина этого участка?
Решение.
Решаем по алгоритму.
1. Кратко записываем условие задачи.
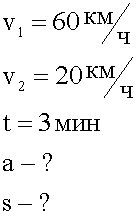
2. Изображаем графически движение, указав пройденный путь и обозначив стрелками скорость, ускорение, направление движения.
![]()
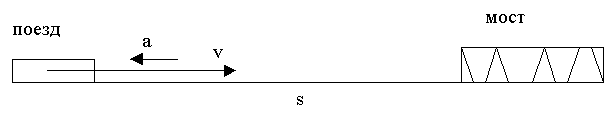
3. Вводим систему отсчета, направляя ось координат по направлению движения.
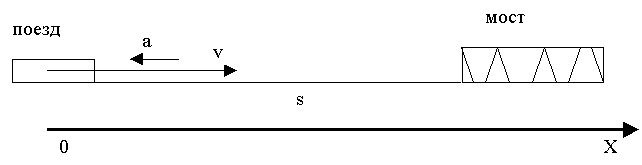
4. Записываем уравнения движения на основе формул из числа вышеуказанных. В данном случае у нас два уравнения: зависимость скорости от времени и зависимость пройденного пути от времени. Первое уравнение мы записываем в виде определения ускорения.
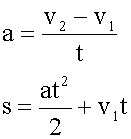
5. Решаем уравнения в общем виде, подставляя во второе уравнение выражение для "a".
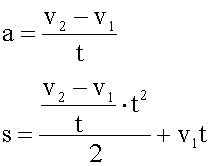
Слегка преобразуя второе уравнение получаем:
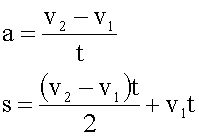
6. Подставляем заданные величины в общее решение, вычисляем. Перед подстановкой переводим время в секунды, а скорость, заданную в км в час в скорость в метрах в секунду.
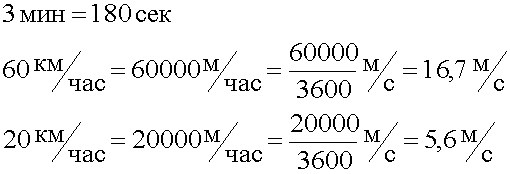
3600 - это количество секунд в одном часе.
Подставляем:
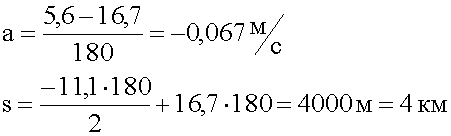
7. Записываем ответ.
Ответ: Ускорение при торможении составило -0,067 м/с, тормозной путь - 4 км.