1. Как движется вертолет массой 5000 кг, если сила тяги 1000 ньютонов, подъемная сила винта - 51000 ньютонов, сила лобового сопротивления - 700 ньютонов.
2. На самолет массой 25000 кг действуют в вертикальном направлении сила тяжести 550 кН и подъемная сила 555 кН, а в горизонтальном направлении - сила тяги 162 кН и сила сопротивления воздуха 150 кН. Найти величину равнодействующей силы.
Тело под действием нескольких сил движется так же, как оно двигалось бы под действием одной силы - равнодействующей заданных сил.
Равнодействующая вычисляется как сумма сил:
![]()
Этому уравнению равносильна система уравнений в проекциях на оси координат:
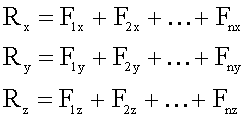
Второй закон Ньютона в векторной записи и в проекциях:
![]()
равносильно:
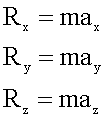
1. Кратко записываем условие задачи.
2. Изображаем условие графически в произвольной системе отсчета, указав действующие на тело (точку) силы.
3. Корректируем и обозначаем на рисунке систему отсчета, вводя начало отсчета времени и уточняя оси координат для сил и ускорения. Лучше направить ось вдоль одной из сил, а отсчет времени начать в момент нахождения тела (точки) в нуле координат.
4. Находим равнодействующую.
5. Записываем в векторной форме второй закон Ньютона и уравнения движения. Уравнения движения и скорости - это зависимости перемещения (пути) и скорости от времени.
6. Записываем в эти же уравнения в скалярной форме: в проекциях на оси координат.
7. Решаем уравнения в общем виде.
8. Подставляем величины в общее решение, вычисляем.
9. Записываем ответ.
Как движется вертолет массой 5000 кг, если сила тяги 1000 ньютонов, подъемная сила винта - 51000 ньютонов, сила лобового сопротивления - 700 ньютонов.
Решение.
1. Кратко записываем условие задачи.
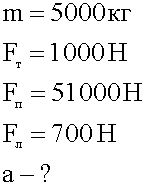
2. Изображаем условие графически в
произвольной системе отсчета.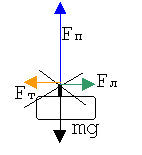
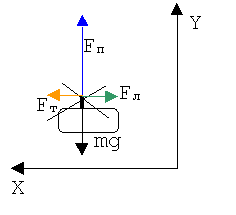
3. Корректируем и обозначаем на рисунке
систему отсчета, вводя начало отсчета времени и направляя одну ось вдоль
силы тяги, а вторую - вдоль подъемной силы.
4. Находим равнодействующую сразу в проекциях на оси. Некоторые проекции сил обращаются в ноль, а некоторые равны величинам векторов, которые сразу пишутся в уравнениях..
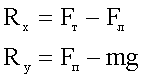
5. Записываем в векторной форме второй закон Ньютона.
![]()
6. Записываем уравнения в скалярной форме: в проекциях на оси координат.
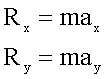
7. Решаем уравнения в общем виде, подставляя в них проекции равнодействующей.
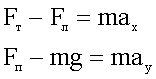
Находим проекции ускорения:
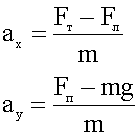
8. Чтобы не создавать громоздких выражений, вычислим проекции ускорения, а затем, используя их, его величину и направление.
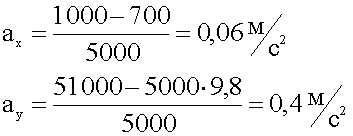
Величину ускорения находим из известного соотношения катетов и гипотенузы прямоугольного треугольника.
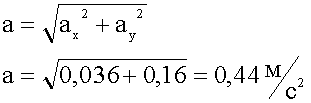
Синус угла между осью абсцисс и направлением ускорения находится из тригонометрических формул.
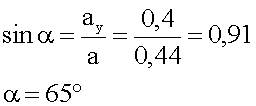
9. Ответ: вертолет набирает высоту с одновременным движением вперед. Ускорение направлено под углом 65 градусов к горизонту и равно 044 м/сек за секунду.
На самолет массой 25 кг действуют в вертикальном направлении сила тяжести 550 кН и подъемная сила 555 кН, а в горизонтальном направлении - сила тяги 162 кН и сила сопротивления воздуха 150 кН. Найти величину равнодействующей силы.
Решение.
1. Кратко записываем условие задачи.
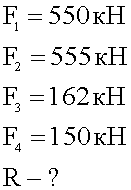
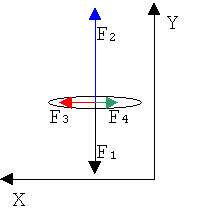
2,
3. Изображаем условие графически , указав действующие на самолет силы и
сразу вводя удобную систему отсчета.
4. Проецируем силы на оси координат
и находим проекции равнодействующей. Сразу учитываем, что некоторые проекции
обращаются в ноль, а некоторые равны величине векторов.
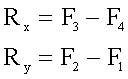
5. Находим величину равнодействующей и ее направление.
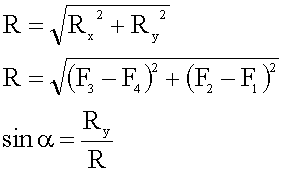
Подставляя конкретные значения, получаем:
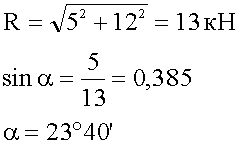
6. Ответ: равнодействующая сил равна 13 кН, направлена под углом двадцать три градуса сорок минут к горизонту.