Типовые задачи:

1. Длина математического маятника 0,8 метра. Чему равен период и частота его колебаний на Земле.

2. Два математических маятника с одинаковыми длинами 1,5 м находятся рядом друг с другом. Амплитуда колебаний первого - 3 см, второго – 6 см. Как различаются периоды их колебаний?

3. Математический маятник совершил 15 колебаний за одну минуту. Каковы период и частота колебаний?

4. Координаты математического маятника изменяются по закону:

Чему равны амплитуда, период и частота колебаний. В формуле все величины выражены в системе СИ.

Краткая теория:

Математический маятник – это абстрактное представление о грузе, имеющем массу, но не имеющем объема, подвешенном на невесомой нерастяжимой нити, длина которой многократно превосходит амплитуду колебаний. Реальным приближением к этому является тяжелый шарик, подвешенный на длинной тонкой нити, совершающий колебания небольшой амплитуды. Математический маятник подчиняется законам движения, по которым можно определить период его колебаний, зная длину нити и ускорение свободного падения в данном месте. Место может быть любое – хоть Луна или Марс, главное – знать ускорение свободного падения. Интересно, что период колебаний математического маятника не зависит от его массы.

Формулы для решения:

Алгоритм решения типовой задачи:

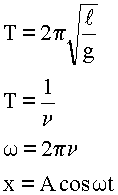
1. Кратко записываем условие, изображаем его графически. На рисунке обозначаем необходимые данные: силы, действующие на маятник, направление его движения, длину нити.
2. Записываем основную формулу для определения периода колебаний математического маятника и другие необходимые формулы колебательного движения. Определяем, какие величины надо найти из других механических соотношений, записываем их.
3. Решаем полученные уравнения в общем виде.
4. Подставляем данные, вычисляем. Перед подстановкой переводим все данные в единую систему.
5. Записываем ответ.

Примеры решения:

Задача 1.

Длина математического маятника 0,8 метра. Чему равен период и частота его колебаний на Земле.

1. Кратко записываем условие, изображаем его графически.

2. Записываем основную формулу для определения периода колебаний математического маятника.

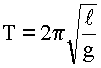
Записываем соотношение между периодом и частотой колебаний.

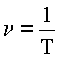
3. Решаем уравнение в общем виде. Формула сразу дает общее решение.

4. Подставляем данные, вычисляем.

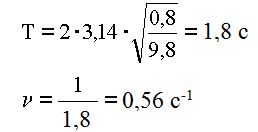
5. Ответ: Период колебаний равен 1,8 секунды, частота – 0,56 колебания в секунду.

Задача 2.

Два математических маятника с одинаковыми длинами 1,5 м находятся рядом друг с другом. Амплитуда колебаний первого - 3 см, второго – 6 см. Как различаются периоды их колебаний?

1. Кратко записываем условие, изображаем его графически.

2. Записываем основную формулу для определения периода колебаний математического маятника.

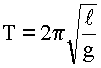
3. Решаем полученные уравнения в общем виде.

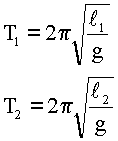
4. Подставляем данные, вычисляем.

Можно вычислять впрямую, а можно сразу сказать, что поскольку длины равны, то и периоды колебаний этих маятников тоже будут равны. Вот как интересно, оказывается, период колебаний математического маятника не зависит от амплитуды.

5. Ответ: Периоды колебаний этих маятников равны между собой.

Задача 3.

Математический маятник совершил 15 колебаний за одну минуту. Каковы период и частота колебаний?

1. Кратко записываем условие, изображаем его графически.

2. Основная формула для определения периода колебаний математического маятника в этой задаче не используется. Используются соотношения для частоты колебаний и их периода.

Частота колебаний – это количество колебаний в единицу времени. Она задана в задаче, только во внесистемных единицах: количество колебаний в минуту. Ее надо преобразовать в системную: в количество колебаний в секунду.

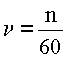
Период колебаний

3. Эти формулы сразу дают решение в общем виде.

4. Подставляем данные, вычисляем.

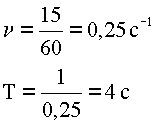
5. Ответ: частота равна четверти колебаний в секунду или 0,25 Гц, период – четырем секундам.

Задача 4.

Координаты математического маятника изменяются по закону

Чему равны амплитуда, период и частота колебаний. В формуле все величины выражены в системе СИ.

1. Кратко записываем условие, изображаем его графически.

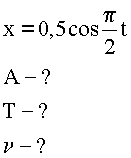
2. Записываем общее уравнение гармонического колебания. Сравниваем заданное уравнение движения маятника с общим уравнением.

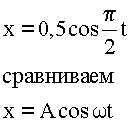
3. Из сравнения получаем:

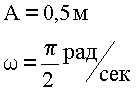
Отсюда легко вычисляется частота и период колебаний.

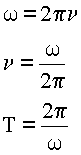
4. Подставляем данные, вычисляем

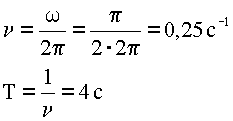
5. Ответ: Амплитуда колебаний равна 0,5 метра, период – четырем секундам, частота – 0,25 Гц.