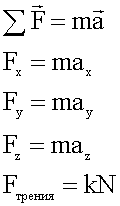
1. Определите характер движения поезда на уклоне рельсового пути 2 градуса, если сила тяги направлена к вершине уклона и равна 2500000 Н, сопротивление движению пренебрежительно мало, а масса поезда составляет 5000 тонн.
2. По наклонной плоскости длиной 10 м и высотой 5 м с вершины без начальной скорости движется тело. Сколько времени будет двигаться тело до основания наклонной плоскости.
3. Тело скользит равномерно по наклонной плоскости с углом наклона 45 градусов. Чему равен коэффициент трения?
4. На вершине наклонной плоскости находится неподвижный блок, через который переброшена невесомая нить с двумя брусками массами 3 и 2 кг. Брусок массой 2 кг, лежащий на наклонной плоскости начинает двигаться вверх без трения и за 2 с проходит путь в 2 м. Определить угол наклона.
Тело на наклонной плоскости движется вниз под действием силы тяжести. Обычно выбирается система координат, одна из осей которой параллельна наклонной плоскости, а другая перпендикулярна и рассматриваются проекции сил на эти направления. Основой решения являются законы Ньютона.
В некоторых задачах, где движутся два тела в разных направлениях иногда целесообразно ввести две системы координат: для каждого тела свою.
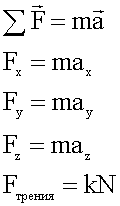
1. Кратко записываем условие задачи.
2. Изображаем условие графически в произвольной системе отсчета, указав действующие на тело силы.
3. Корректируем и обозначаем на рисунке систему отсчета, вводя начало отсчета времени и уточняя оси координат для сил и ускорения. Лучше направить одну ось вдоль наклонной плоскости, вторую - перпендикулярно ей, а отсчет времени начать в момент нахождения тела в нуле координат.
4. Записываем в векторной форме второй закон Ньютона и уравнения движения. Уравнения движения и скорости - это зависимости перемещения (пути) и скорости от времени.
5. Записываем в эти же уравнения в скалярной форме: в проекциях на оси координат.
6. Решаем уравнения в общем виде.
7. Подставляем величины в общее решение, вычисляем.
8. Записываем ответ.
Определите характер движения поезда на уклоне рельсового пути 2 градуса, если сила тяги направлена к вершине уклона и равна 2500000 Н, сопротивление движению пренебрежительно мало, а масса поезда составляет 5000 тонн.
Решение.
1. Кратко записываем условие задачи.
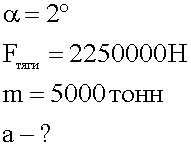
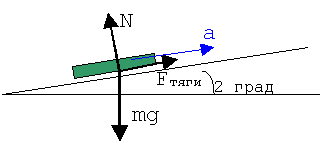
2. Изображаем условие графически.>
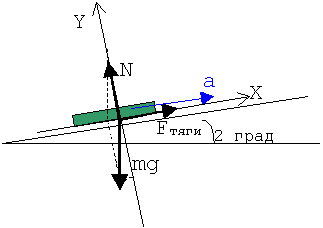
3. Обозначаем на рисунке систему отсчета.
Направляем одну ось вдоль наклонной плоскости, вторую - перпендикулярно
ей, отсчет времени начинаем в момент нахождения поезда в нуле координат.
4. Записываем в векторной форме второй
закон Ньютона. 
5. Записываем уравнения в проекциях на оси координат, учитывая, что некоторые проекции обращаются в ноль.
6. Решаем уравнения в общем виде.
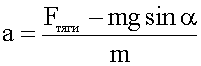
7. Подставляем величины в общее решение, вычисляем.
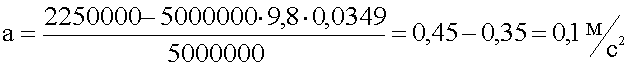
8. Ответ: ускорение равно 0,1 м/с2.
По наклонной плоскости длиной 10 м и высотой 5 м с вершины без начальной скорости движется тело. Сколько времени будет двигаться тело до основания наклонной плоскости.
Решение.
1. Кратко записываем условие задачи.
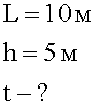
2. Изображаем условие графически, указав действующие на тело силы.
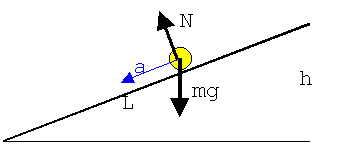
3. Корректируем и обозначаем на рисунке систему отсчета, вводя начало отсчета времени и уточняя оси координат для сил и ускорения. Лучше направить одну ось вдоль наклонной плоскости, вторую - перпендикулярно ей, а отсчет времени начать в момент нахождения тела в нуле координат.
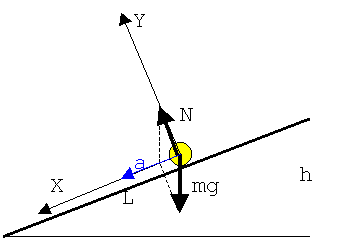
4. Записываем в векторной форме второй закон Ньютона и уравнения движения.
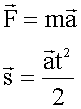
5. Записываем уравнения в проекциях на оси координат.
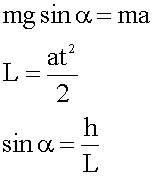
6. Решаем уравнения в общем виде. Из первого уравнения находим ускорение:
Подставляем во второе, учитывая выражение для синуса угла из третьего уравнения:
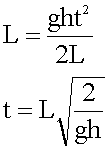
7. Подставляем величины в общее решение, вычисляем.
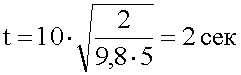
8. Ответ: на спуск тела потребуется 2 секунды.
Тело скользит равномерно по наклонной плоскости с углом наклона 45 градусов. Чему равен коэффициент трения?
Решение.
1. Кратко записываем условие задачи.
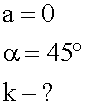
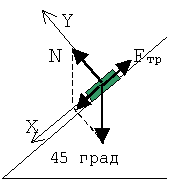2, 3. Изображаем условие графически,
указав действующие на тело силы. Сразу обозначаем систему отсчета, направляя
одну ось вдоль наклонной плоскости, а вторую - перпендикулярно ей.
4. Записываем в векторной форме второй
закон Ньютона.
5. Записываем уравнения в проекциях на оси координат.
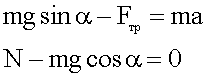
6. Решаем уравнения в общем виде. По условию ускорение равно нулю, поэтому:
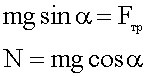
Сила трения определяется как 
Откуда имеем: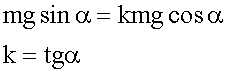 
7. Подставляем величины в общее решение, вычисляем.
8. Ответ: коэффициент трения равен 1.
На вершине наклонной плоскости находится неподвижный блок, через который переброшена невесомая нить с двумя брусками массами 3 и 2 кг. Брусок массой 3 кг, лежащий на наклонной плоскости начинает двигаться вверх без трения и за 2 с проходит путь в 2 м. Определить угол наклона.
Решение.
1. Кратко записываем условие задачи.
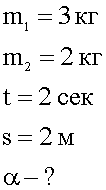
2. Изображаем условие графически, указав действующие на тела силы.
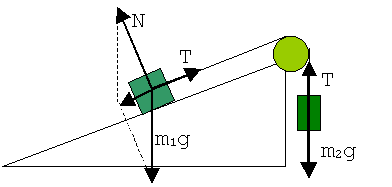
3. Обозначаем на рисунке системы отсчета. Для каждого тела выбираем свою. В первой системе направляем одну ось вдоль наклонной плоскости, вторую - перпендикулярно ей. Во второй системе достаточно ввести одну ось вдоль движения.
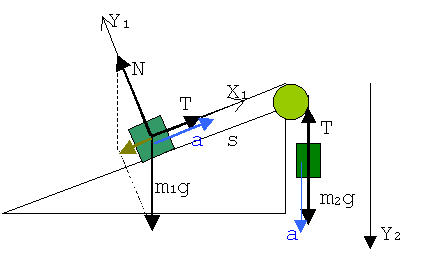
4. Записываем в векторной форме второй закон Ньютона для каждого тела и уравнение движения для первого тела.
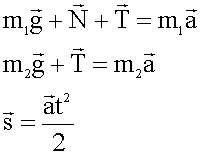
5. Записываем эти же уравнения в проекциях на оси координат. Учитываем сразу, что некоторые проекции обращаются в ноль. Мы полагаем, что натяжение в разных местах нити одинаковое, а ускорения грузов равны, так как грузы связаны между собой.
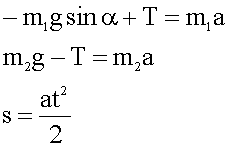
6. Решаем уравнения в общем виде. Складываем два первых уравнения, а из третьего сразу находим ускорение.
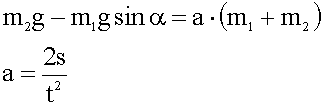
Из первого уравнения находим синус угла, подставляем выражение для ускорения.
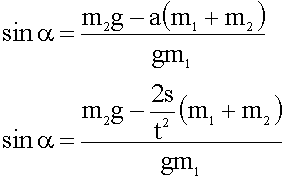
7. Подставляем величины в общее решение, вычисляем.
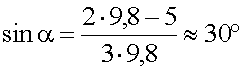
8. Ответ: угол наклонной плоскости 30 градусов.